Colour Changing Fibres Predict a Knot's Strength

With help from spaghetti and color-changing fibers, a new mathematical model predicts a knot’s stability. In sailing, rock climbing, construction, and any activity requiring the securing of ropes, certain knots are known to be stronger than others. Any seasoned sailor knows, for instance, that one type of knot will secure a sheet to a headsail, while another is better for hitching a boat to a piling.

MIT mathematicians and engineers have developed a mathematical model that predicts how stable a knot is, based on several key properties, including the number of crossings involved and the direction in which the rope segments twist as the knot is pulled tight.

Pressure’s color

In 2018, Kolle’s group engineered stretchable fibers that change color in response to strain or pressure. The researchers showed that when they pulled on a fiber, its hue changed from one color of the rainbow to another, particularly in areas that experienced the greatest stress or pressure.

Kolle, an associate professor of mechanical engineering, was invited by MIT’s math department to give a talk on the fibers. Dunkel was in the audience and began to cook up an idea: What if the pressure-sensing fibers could be used to study the stability in knots?

Mathematicians have long been intrigued by knots, so much so that physical knots have inspired an entire subfield of topology known as knot theory — the study of theoretical knots whose ends, unlike actual knots, are joined to form a continuous pattern. In knot theory, mathematicians seek to describe a knot in mathematical terms, along with all the ways that it can be twisted or deformed while still retaining its topology or general geometry.

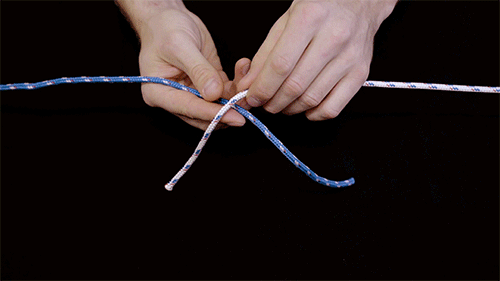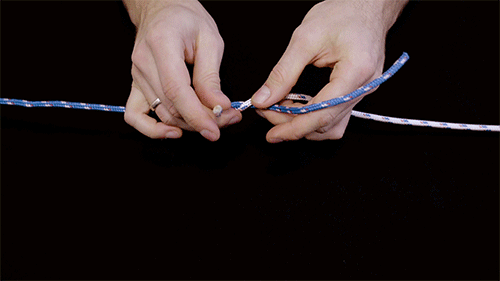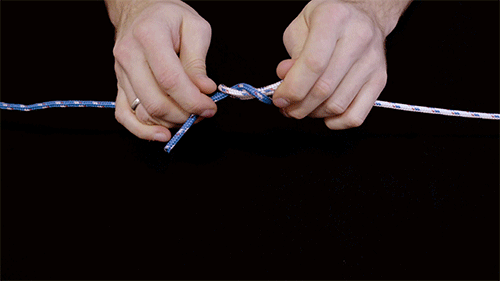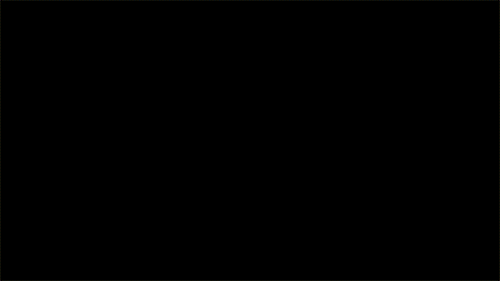
With confidence in their model, Patil then simulated more complicated knots, taking note of which knots experienced more pressure and were therefore stronger than other knots. Once they categorized knots based on their relative strength, Patil and Dunkel looked for an explanation for why certain knots were stronger than others. To do this, they drew up simple diagrams for the well-known granny, reef, thief, and grief knots, along with more complicated ones, such as the carrick, zeppelin, and Alpine butterfly.

Each knot diagram depicts the pattern of the two strands in a knot before it is pulled tight. The researchers included the direction of each segment of a strand as it is pulled, along with where strands cross. They also noted the direction each segment of a strand rotates as a knot is tightened.

They also found that a knot can be made stronger if it has more “circulations,” which they define as a region in a knot where two parallel strands loop against each other in opposite directions, like a circular flow.