As far as I remember that the first time I heard of the term “Strain” was probably in the Engineering materials module at the university. While learning about the tensile test, the lecturer was drawing some parallel lines to a slope that was claimed to be a result of the “tensile test”, and writing strain values, which was weirdly unitless, on the horizontal axis. Initially, these terms were so abstract that I was having issues to image what exactly the strain meant. However, after years I had so much work on determining materials’ mechanical behaviours and properties both in academia and industry, these really help me to answer the questions, what is the exact difference between Stress and Strain, do we merely use stress in calculations rather than a strain?
First of all, we should understand what a tensile test stands for!
Tensile test
The uniaxial tensile test may very well be the most useful material characterization test available. This test is done with standard size samples (according to EN or ASME) until the material is broken. Of course, you can have this test with non-standard samples however, the calculations and measurements will be different to find out the tensile strength or yield strength of the material. Additional, in the event that your sample has holes, notches or surface defects, these will highly affect results, and your tensile test will be only valid for your specific case. Therefore, standard test samples are used in determining the strength of materials.

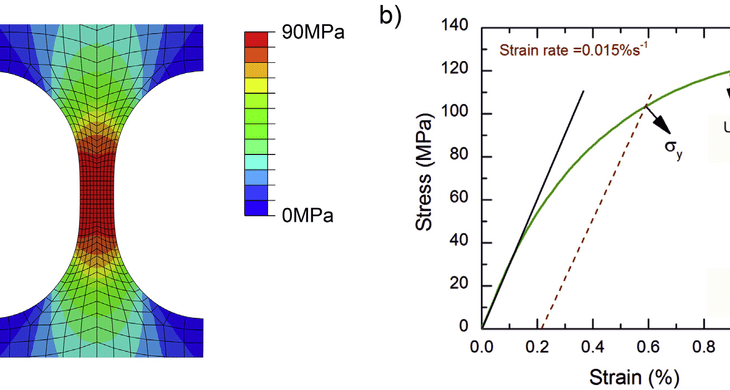
It works simply by continuously measuring the force required to elongate a test specimen by increasing increments until it fractures. The test measures a number of important material properties as illustrated below. Most importantly, it generates stress-strain curves, which are the unique identifiers of each material tested (each material’s DNA, so to speak). Figure 2 shows a stress-strain graph obtained from a tensile test. In reality, mostly we get a force and displacement graph out of the tensile test machine, but these values can easily be interpreted to stress and strain graph by known parameters of the sectional area and the initial length of the sample. I would like to have your attention here, while the test sample is elongating, we expect that the sectional area to be reduced, so therefore, the stress calculation based on force divided by the initial section area or actual section area will bring two terms of true or engineering stress-strain curve. But at the moment we accept that the sectioned area does not change.
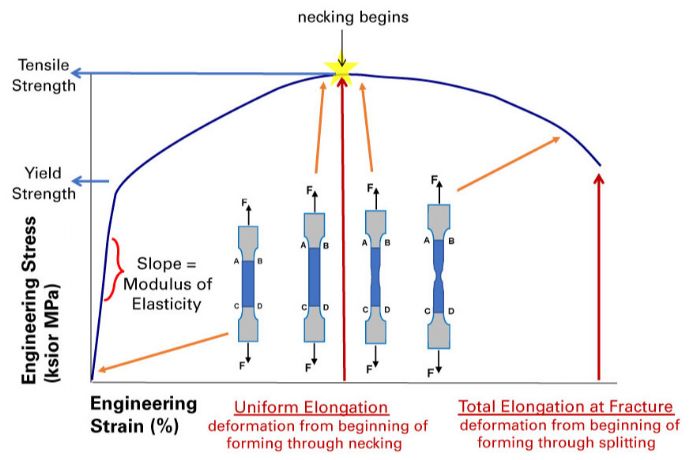
Engineering stress is defined simply as instantaneous force divided by the original cross-sectional area of the test specimen. Engineering strain is simply the change in the test specimen length divided by the original length, usually specified as a percentage or mm/mm (unitless because it is a kind of ratio). As the test proceeds, the force required to elongate the specimen increases linearly (for most materials) up to a point known as the proportional limit. On this slope, the material will usually return to its original, undeformed shape when the load is removed. This is referred to as elastic behaviour. The slope of the curve up to this point is known variously as the elastic modulus, Young’s modulus, or modulus of elasticity.
The yield point is the point after permanent deformation will occur and the part if unloaded will not return to its original shape. Usually, the proportional limit occurs on the stress-strain diagram slightly before the yield point. Sometimes they are so close that people use them interchangeably. However, we should know that Yield point and proportional limits are the same parameters.
So up to Yield point/strength we highly benefit from Hooke’s Law in which strain is proportional to the stress as follows;
\sigma=\epsilon \Epsilon
where sigma is stress, epsilon is strain and E is Young’s modulus.
We often check our designs based on yields strength by adding a safety factor and deciding whether it is safe to build it. However, I have some bad news. The yield strength is often very unclear in tensile tests, particularly very difficult to determine if you have a ductile material such as copper. Here is an example of test data showing tensile test results of copper material.
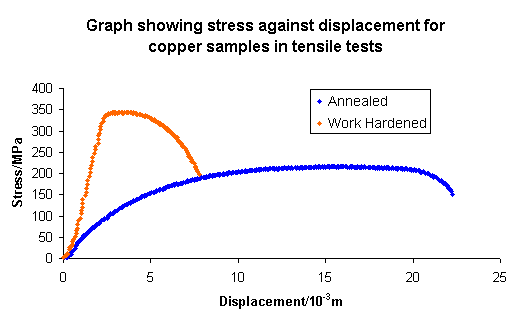
From the figure, it is difficult to determine a straight line showing Hooke’s law behaviours and a yield point. Therefore in these situations, a proof yield strength is used. The 0.2% offset yield strength (0.2% OYS, 0.2% proof stress, RP0.2, RP0,2) is defined as the amount of stress that will result in a plastic strain of 0.2%.
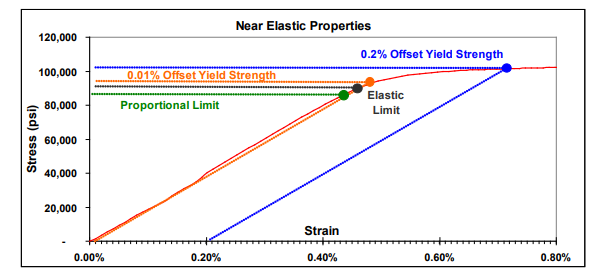
This is illustrated by the blue line in Figure 4 above This is the yield strength that is most often quoted by material suppliers and used by design engineers. If a different permanent set is specified, then there will be a different yield strength associated with that strain level. For example, the orange line in the figure below would represent the 0.01% offset yield strength. In some cases, particularly with low strength rod or wire, it is difficult to accurately measure the plastic strain. In this case, the total strain is measured, and the 0.5% extension under load yield strength (0.5% EUL, RT0.5) is listed instead.
However, if the stress is high enough, the object will permanently deform. This is referred to as plastic behavior. The elastic limit on a stress-strain curve is the point where the behaviour of the material switches from elastic to plastic. If the stress (and therefore strain) applied to a material is lower than the elastic limit, both the stress and strain will return to zero (recover) when the load is removed. If, however, the elastic limit is exceeded, only the elastic strain will be recovered, and the plastic strain will remain as a permanent set. The stress in the material will unload along a path parallel to the elastic modulus. From this point on the Hooke’s law will no longer be valid. There will be other modules to determine the stress-strain relationship in this area, they are exponential equations or multilinear equations.
Stress or Strain
Here is the most important point to decide whether stress or strain is more reliable in our calculations after exceeding the proportional or yield point of the material. If you have a quick look at Figure 4, we can say that we can either use strain or stress in our calculations up to the elastic limit because they are proportional to each other. However, after the elastic limit is reached, even though small changes in stress could cause the strain to double. Therefore, you can realise that most of the plastic deformation problems are expressed with strain parameters rather than stress values. Because when permanent deformation exists it is less reliable to talk with stress in the material. You can see an example that low cycle fatigue problems are expressed with the strain-life method while high-cycles fatigues are stress-life methods.
Conclusion
So to answer the question we asked at the beginning of the article, both stress and strain parameters are important in determining the mechanical behaviours of materials. As We engineers love talking with certain numbers and proofs. While the stress and strain transformation can be easily done by Hooke’s law in the elastic region, strain is a more reliable parameter to talk about materials behaviours when a plastic deformation exists.
References
1-https://materion.com/-/media/files/alloy/newsletters/technical-tidbits/issue-no-47—yield-strength-and-other-near-elastic-properties.pdf
2- https://www.quora.com/What-is-the-difference-between-proportional-limit-and-yield-point#:~:text=The%20yield%20point%20is%20the,that%20people%20use%20them%20interchangeably.
3- https://materion.com/-/media/files/alloy/newsletters/technical-tidbits/issue-no-45—stress-strain-concepts-revisited—part-1.pdf