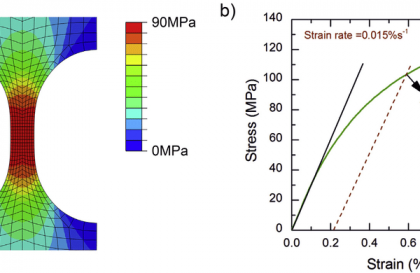
In the realm of engineering and materials science, ensuring the structural integrity of various components and structures is of utmost importance. From bridges and buildings to airplanes and pipelines, the potential for fractures and failures poses significant risks. Enter fracture mechanics, a field that delves into the study of how materials behave when subjected to stress and strain, aiming to predict and prevent catastrophic failures. In this article, we will explore the fundamentals of fracture mechanics and its applications, shedding light on its significance in maintaining safety and reliability.
Defining Fracture Mechanics
Fracture mechanics is a branch of materials science that focuses on the study of cracks and their propagation within materials under various loading conditions. It seeks to understand the behavior of materials when subjected to external forces and stresses, and how these forces can lead to the initiation and growth of cracks. By analyzing the characteristics and behavior of these cracks, fracture mechanics aims to predict the conditions under which structural failure may occur.
The Role of Stress and Strain
Understanding the relationship between stress and strain is crucial in fracture mechanics. Stress refers to the internal forces acting within a material, while strain describes the deformation experienced by the material in response to those forces. Fracture mechanics investigates the effects of stress on materials, considering parameters such as tensile, compressive, and shear stress, as well as their distribution and magnitude.
Modes of Fracture
Fracture can occur in different modes, each having its distinct characteristics. The primary fracture modes studied in fracture mechanics are:
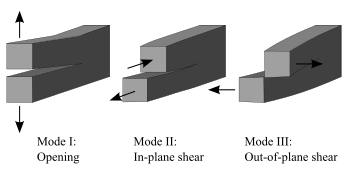
a) Mode I: Also known as the opening mode or tensile mode, Mode I fracture occurs when the crack surfaces move apart due to tensile forces acting perpendicular to the crack plane.
b) Mode II: Referred to as sliding mode or shear mode, Mode II fracture takes place when the crack surfaces slide past each other due to shear forces acting parallel to the crack plane.
c) Mode III: Known as the tearing mode or tearing shear mode, Mode III fracture happens when the crack surfaces move parallel to the crack plane under shear forces.
Understanding these fracture modes and their specific characteristics aids in determining the appropriate analysis and remedial actions to ensure structural integrity.
Stress Intensity Factor, K, (SIF) Fracture Toughness
One of the fundamental concepts in fracture mechanics is the stress intensity factor (SIF). It quantifies the severity of stress near the crack tip and provides a measure of crack growth tendency. Fracture toughness, on the other hand, represents the resistance of a material to fracture and is a critical parameter in assessing its structural reliability.
A general form of the stress intensity is expressed depending on geometry as follows
K=C\sigma \sqrt{\pi.a}f(a/w)where w is the width of the specimen, a is the crack size and C and f(a/w) are constants determined by stress analysis.
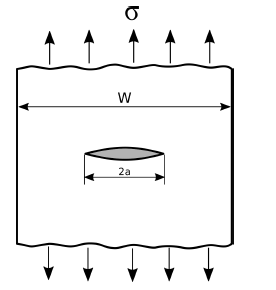
However, a number of different approaches are available for stress intensity calculation depending on the position of the crack (centered, tip etc) and ratio of a/w with a various accuracy.
Irwin suggested a solution for centered cracks with accuracy of 5 % for a/w ≤ 0.25;
K_{1}=\sigma\sqrt{\pi a}\sqrt{\frac{w}{\pi a}tan\frac{\pi a}{w}}Brown found another approximation with 0.5 % accuracy for a/w ≤ 0.35;
K_{1}=f(a/w)\sigma\sqrt{\pi.a}f(a/w)=1+0.256\frac{a}{w}-1.152(\frac{a}{w})^2+12.2(\frac{a}{w})^3A simpler and more accurate expression was suggested by Feddersen with accuracy of 0.3 % for a/w ≤ 0.35;
K_{1}=\sigma\sqrt{\pi.a}\sqrt{{sec}\frac{\pi.a}{w}}Stress intensity approaches are also applied to single or double-edge cracked samples.The geometry of single and double edge crack is shown below.
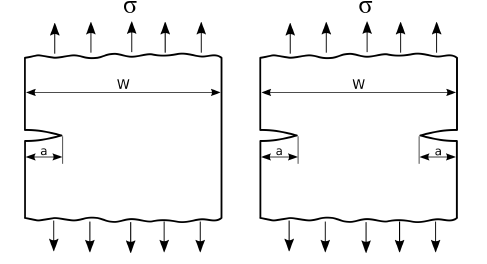
For single and double notched edge cracks, following expressions were proposed ;
Single edge notched crack:
K_{1}=\sigma\sqrt{\pi.a}(1.122-0.231\frac{a}{w}+10.550(\frac{a}{w})^2-21.710(\frac{a}{w})^3+30.382(\frac{a}{w})^4)Double edge notched crack:
K_{1}=\sqrt{\pi.a}\frac{(1.122-1.122\frac{a}{w}-820(\frac{a}{w})^2+3.768(\frac{a}{w})^3-3.040(\frac{a}{w})^4)}{\sqrt{1-\frac{2.a}{w}}}Fracture toughness is considered a material property and is determined by experimental tests . The first fracture toughness test was standardized with E399 by American Society for Testing and Materials (ASTM) in the United States. Later, the standard terminology of fracture testing was defined in ASTM E1823 , and the standard test method for measurement of fracture toughness was enlarged in ASTM E1820 . According to ASTM E1823, the fracture toughness of a material is determined for the opening mode (Mode I).
Applications of Fracture Mechanics
Fracture mechanics finds widespread applications in various industries, contributing to the safety and durability of critical structures and components. Some notable applications include:
a) Aerospace Industry: Fracture mechanics plays a pivotal role in ensuring the structural integrity of aircraft components, such as wings, fuselage, and engine parts, helping to prevent catastrophic failures during flight.

b) Civil Engineering: Bridges, buildings, and dams rely on fracture mechanics principles to assess the potential for crack growth and structural instability, enabling engineers to design safer structures and implement timely maintenance.

c) Oil and Gas Industry: Pipelines and pressure vessels are subjected to extreme conditions and may develop cracks over time. Fracture mechanics aid in assessing the integrity of these structures, guiding inspection and maintenance protocols to prevent hazardous leaks or ruptures.

Conclusion
Fracture mechanics is a vital discipline in engineering and materials science that seeks to unravel the behavior of materials under stress and strain, specifically focusing on cracks and their propagation. By understanding the fundamental concepts and applying fracture mechanics principles, engineers can assess the potential for fractures and failures, ensuring the safety and reliability of various structures and components. With ongoing advancements in materials technology and analysis techniques, fracture mechanics continues to play a pivotal role in safeguarding our built environment and fostering innovation in engineering design.