This week we are welcoming Michal Szulewski from Poland with his fantastic home-made experimental rig for linear buckling and FE solutions. Let’s read his fantastic work from his speech;
In my previous publication, I was checking the correlation between hand calculations, FEA and experiment results of static beam deflection. This time I wanted to check something more demanding – buckling.
I kept my standard of experiments, it means an analytical solution, a numerical solution FEA, and experiment and comparison. The goal of this study was to verify the possibility of buckling of a solid rod with Euler linear theory usage.
Experimental Setup
I started building a test stand. I spent some hours on thinking, what components can I use to assembly a homemade strength machine. Of course, I could contract out experimental procedure to the laboratory or buy a machine, but I wanted to prove myself, that I can do everything my own at home conditions. After spending some days on exploring web auctions of car components, pneumatic and steel accessories and making some hand calculations I created by my own machine visible in the Fig.1

Main components of the machine are a pneumatic two-way actuator and a hose, a control valve, square steel profiles, a pressure chamber from car’s suspension, a pump and manometers.
Like in my previous experiment, this time also material’s data were a little bit problematic because detailed information was very hard to get – specimens were bought in a DIY store. But to perform Euler linear buckling calculations I could use some approximations. The material used was aluminium alloy PA38.
Analytical Solutions
The first point of analysis was checking the critical slenderness of the material lambda crit:
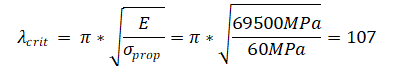
Young Modulus E is a material constant, so it is easy to choose its value. It is almost the same for all aluminium alloys. The proportionality limit was not so obvious, because it is strongly connected e.g. with heat treatment. For PA38 proportionality limit fits in the range 60 – 160MPa. I assumed, that I had the weakest alloy with 60 MPa proportionality limit. I received 107 of slenderness. For 160MPa critical slenderness is equal to 65.5
Linear Euler buckling theory works only for slenderness value higher than critical, so for the experiment, I had to choose geometry dimensions, which respected critical slenderness. I used solid circle rod with 350mm of length and 5mm of diameter. For this geometry we have slenderness lambda s as below:

Slenderness ratio 280 > 107 and 65.5, so Euler theory is working for all range of proportionality limits of PA38 for specified geometry.
The next step was to calculate critical stress and force as below:
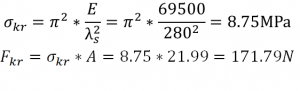
FEM Analysis
To perform FEM analysis I decided to use a demo version of Strand7 software, which allows performing some simple cases for free. I created boundary conditions, which corresponded to conditions used in the analytical solution. The column was built with five 1D elements. I applied 100N compression force in the vertical direction like in the figure below:
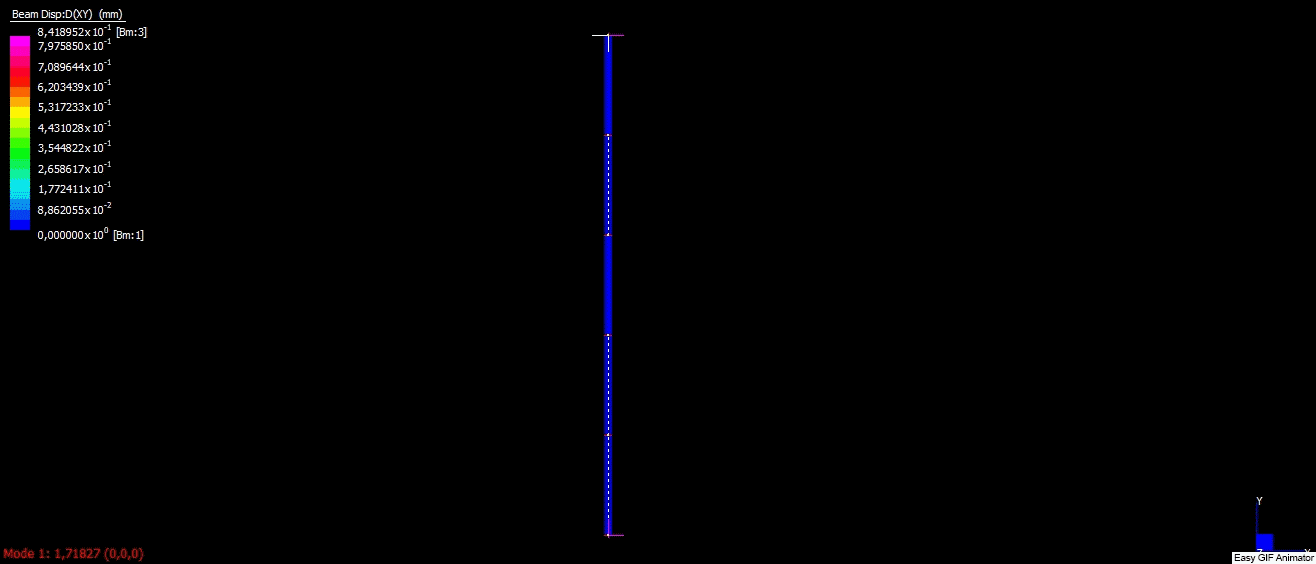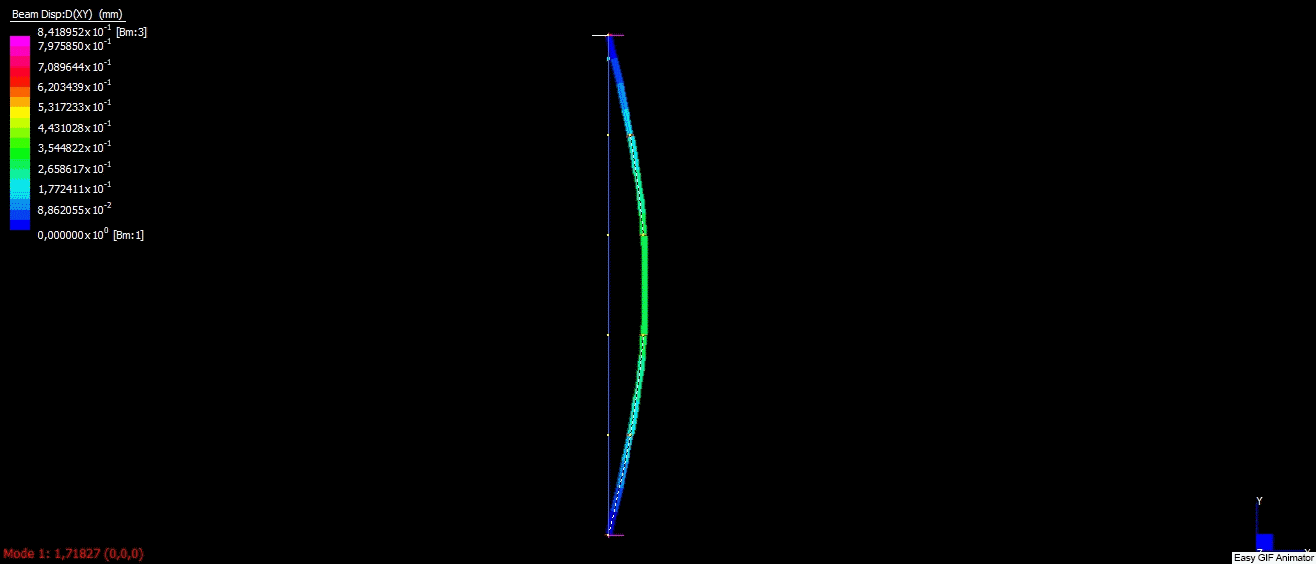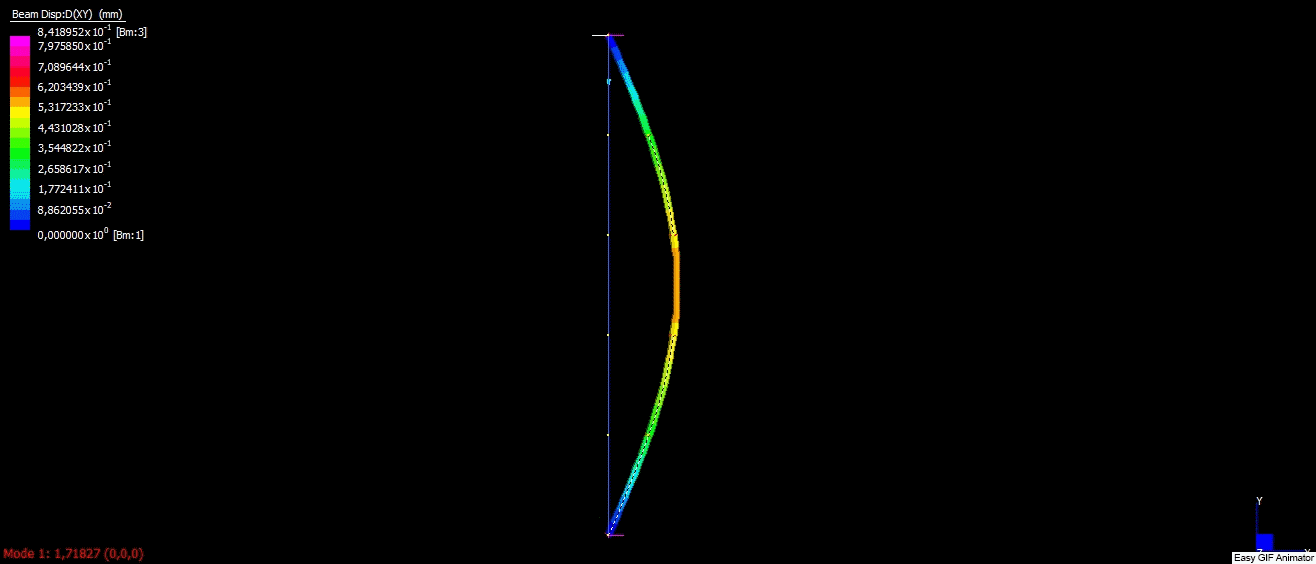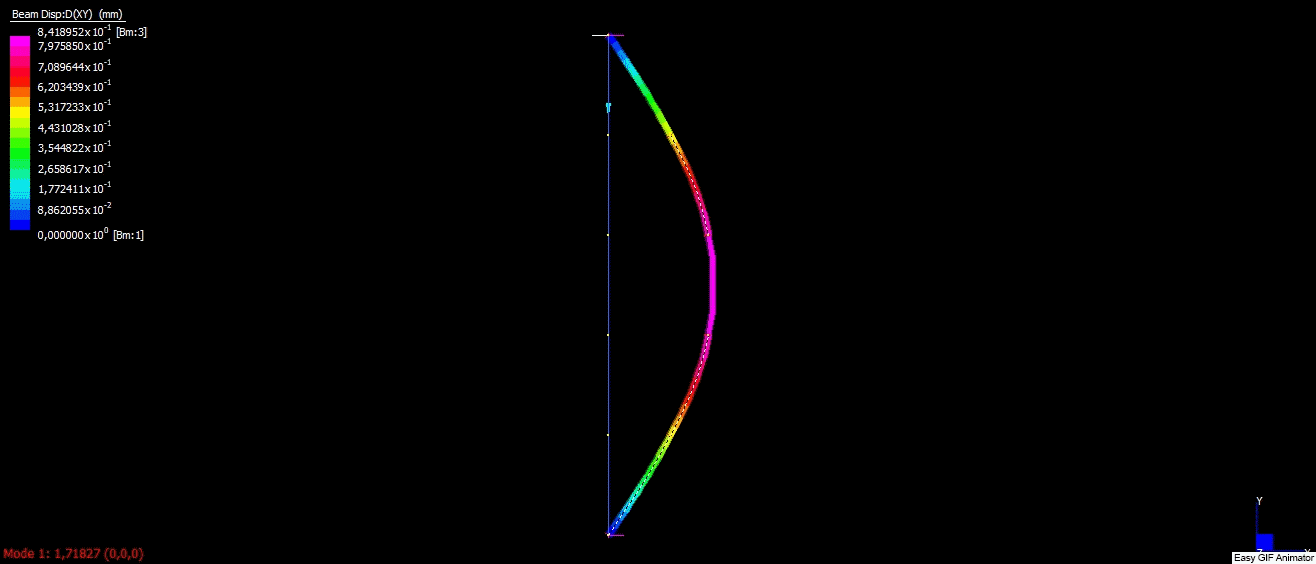
After solving igenvalue problem, solver returned multiplier = 1.7183. After multiplying it by compression force I received critical force as below:
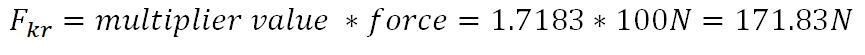
The last step was performing an experiment. The piston in actuator had diameter d = 50mm. To create ~172N of force I had to create ~0.0875MPa in my pressure system. It is equal to ~0,88 bar
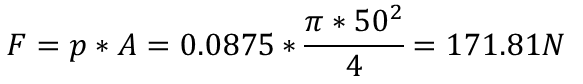
Results of the experiment below (to see a detailed view of the picture and manometer, the open picture below in a new card by right click mouse on it):

I received a buckle shape of the rod at around 0.9 bar ~0.09MPa. Close to 1 bar of pressure, rod damaged in a nonlinear way. I recorded a video to illustrate it more detailed. You can see it below:
I did several tests to check the repeatability of my procedure and machine. Below you can see some specimens after tests:

Summary
Summary of analysing critical compression force:
- Hand calculations: 171.79N
- FEA: 171.83N
- The experiment: ~0.9-1.0 bar => 176-196N (manometer scale was not precise enough to check decimal)
Relative errors of my analysis
- Hand calculations vs FEA:
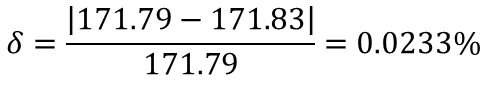
- Hand calculations vs an experiment:
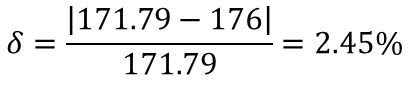
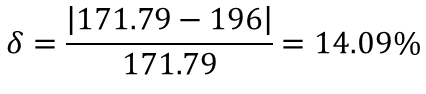
The relative error between the analytical solution and experiment was in the range between ~2.5-14%








