Nomenclature
Natural Frequency: This value is typically given in Hertz (Hz).
Damping Ratio: This value is typically represented as a percentage of the critical damping and therefore given in percent (%)
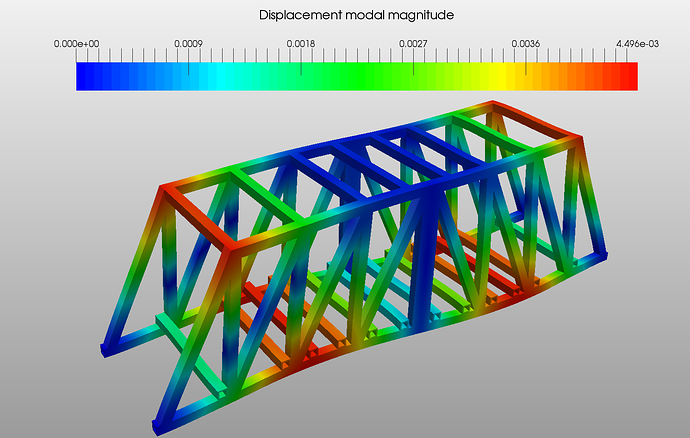
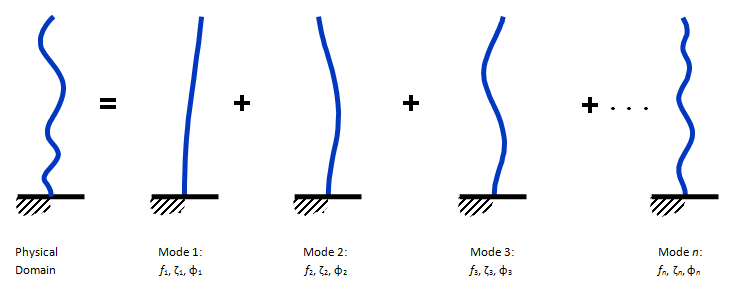
Mode shape: The geometrical way the structure moves in this particular mode of vibration.
Everything vibrates! This is a fact of life and modal analysis is the technique used to characterize how structures behave dynamically.
The modal analysis provides an overview of the limits of a system’s responses. For example, it gives a general answer to the question of what are the limits of the system response (such as when and how much maximum displacement is) for a given input (such as a load applied at a given amplitude and frequency). Every object has a natural frequency (or resonant frequency) at which it can vibrate. This frequency is also the frequency at which the object will allow energy transfer from one form to another (here from vibration to kinetics) with minimal loss. As the frequency approaches the resonant frequency, the amplitude of the system’s response increases asymptotically to infinity. In other words, the frequency at which the amplitude goes to infinity is calculated with modal analysis
Modal analysis is an analysis performed to determine the characteristics of the system, without any external loading. In this case, if we consider the generalized equation of motion;
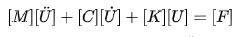
For structures, the damping amount is generally neglected as it is below 10% and if it is considered that there is no external loading;
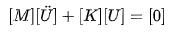
It is observed that the natural frequencies of the system depend on mass and stiffness matrices.
The purpose of modal analysis in general;
- Defining the natural frequencies and mode shapes of the system
- To check the connections between components if there are rigid modes in the system
- To determine whether the constraints are correct in the system
- Determining the behaviour of the system under dynamic loads
Knowing the natural frequency of a structure helps to know the operating frequencies of the system under dynamic loading conditions and to predict its responses (such as resonance) at these frequencies.
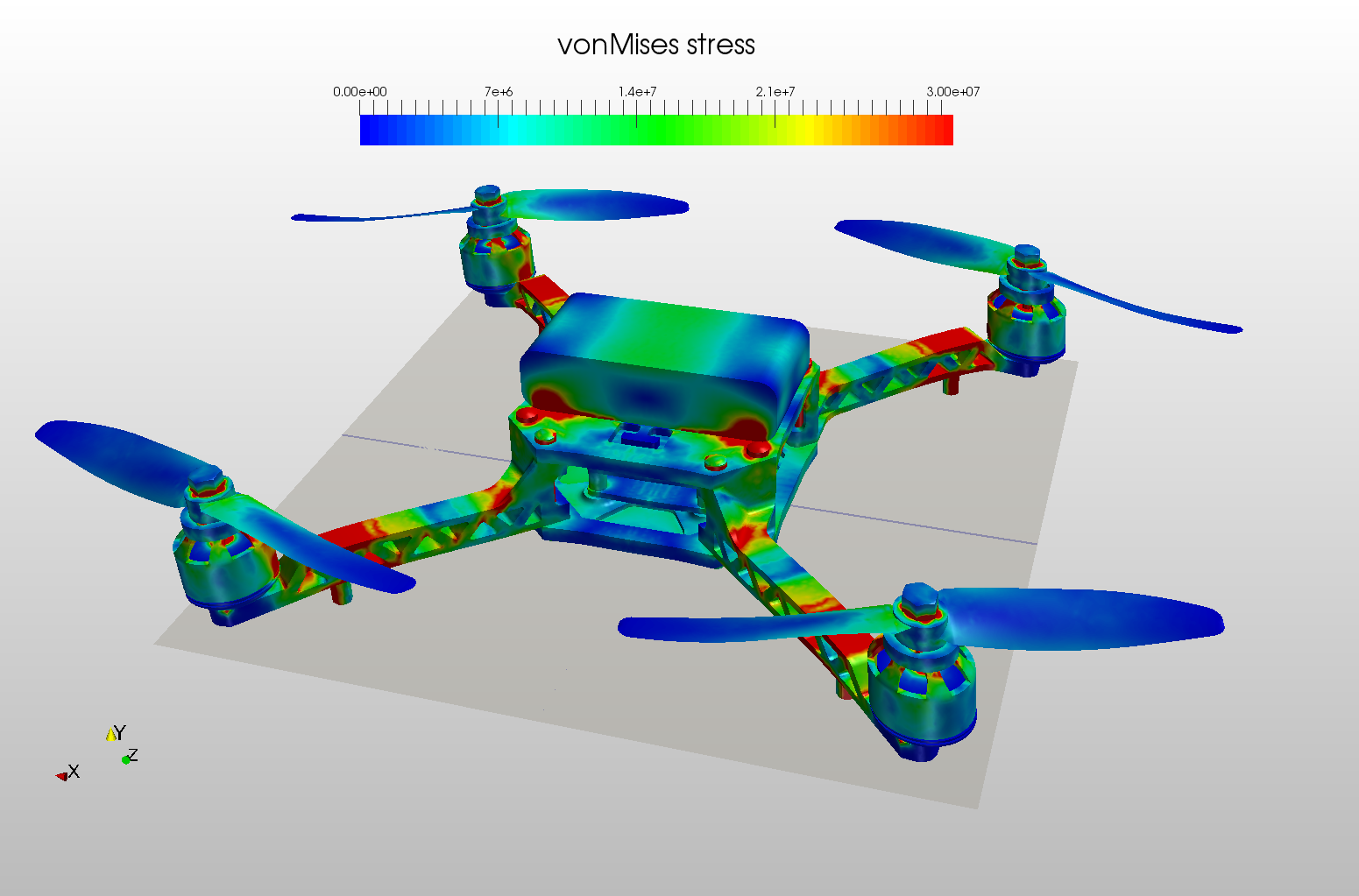
When performing modal analysis with the finite element method, it is important to install a model in size and shape that best represents the mode shapes of the system. Particularly, the elements must represent the geometry in the best way to correctly detect natural frequencies and to determine the mode shapes at these frequencies (such as bending, torsion mode).
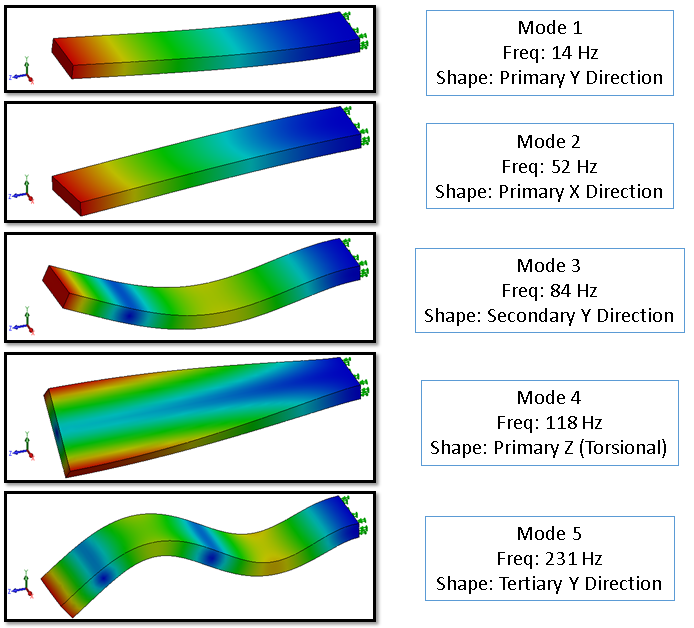
So what should be done to improve the working conditions of the system as a result of modal analysis?
As a result of the modal analysis, two important results we should pay attention to; eigenvalues and strain energy density values. Optimisation is required at the points where these values are maximum. At the points where the eigenvalue is maximum, we need to decrease the mass and increase the stiffness. So ;
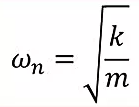
The natural frequency value is increased and the system avoids resonance at higher frequencies.
Another result is strain energy density. At the points where strain energy density is maximum, it is necessary to increase the stiffness and strengthen the region.
In this way, we can improve the working conditions by increasing the natural frequency values, which are characteristic of the system, before dynamic analysis.
The modal analysis also plays an important role when dynamic analysis needs to compare with physical tests. It allows identifying the correct equipment and the correct location to be used for accelerometers and strain gauges. It helps to understand the test results during testing and to associate the virtual model with the prototype.