Is Your Mesh Good Enough?

Finite element solutions are becoming vital for complex engineering systems that are not simple to analyze by using old traditional methods. Comparing to theoretical approaches, FE models are capable to deal with much more intricate multiphysics problems. However, two crucial steps,  meshing and its quality play an important role in your results.

How do I know if my mesh is good enough?

Finite element preprocessors have come a long way over the years, to the point where users with minimal training can create meshes that appear “good”. But, how can you really know if the mesh is good enough for your analysis? Meshes that are “good enough” are ones that produce results with an acceptable level of accuracy, assuming that all other inputs to the model are accurate.

Mesh density is a significant metric used to control accuracy (element type and shape also affect accuracy). Assuming no singularities are present, a high-density mesh will produce results with high accuracy. However, if a mesh is too dense, it will require a large amount of computer memory and long run times, especially for multiple-iteration runs that are typical of nonlinear and transient analyses.

There are several ways to check your mesh quality;

• Software mesh control features (you can check the global mesh control in Ansys here)
• Mesh Metrics
• Convergence Analysis
• Test data or to theoretical values

Unfortunately, test data and theoretical results are often not available. So, other means of evaluating mesh quality are needed.

Mesh Metrics

“Mesh Metrics” is one of the most useful features in determining the correct shape and size of the elements. You can find a range of criteria for quality check of your mesh, however, in this article, we will only explain, Aspect Ratio, Jacobian Ratio and Skewness.

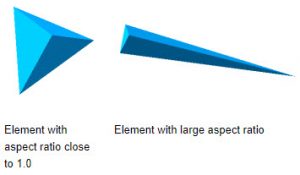
Aspect Ratio

The Aspect Ratio quantifies the quality of the elements, where 1 is a perfectly shaped tetrahedral element and the element shape is worse with a higher Aspect Ratio. You can see this in the image to the left. The aspect ratio is defined as the ratio of the shortest length of the element to the longest length of the element.

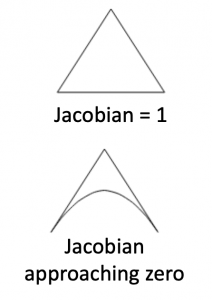
Jacobian

Jacobian (also called Jacobian Ratio) is a measure of the deviation of a given element from an ideally shaped element. The jacobian value ranges from -1.0 to 1.0, where 1.0 represents a perfectly shaped element.

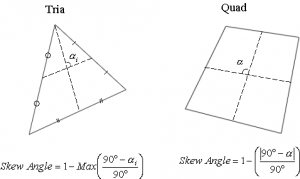
Skewness

Skewness is the Angular Measure of Element quality with respect to the Angles of Ideal Element Types. It is one of the Primary Qualities Measures of FE Mesh. Skewness determines how close to ideal (i.e., equilateral or equi-angular) a face or cell is. The acceptable range of skewness is “0 to 0.5”.

Convergence Analysis

The most fundamental and accurate method for evaluating mesh quality is to refine the mesh until a critical result, such as the maximum stress in a specific location converges (i.e. it doesn’t change significantly with each refinement).   An example is shown in Figure 1, where a 2D bracket model is constrained at its top end and subjected to a shear load at the edge on the lower right.  This generates a peak stress in the fillet, as shown.  The curve shows that as the mesh density increases, the peak stress in the fillet increases.  Ultimately, increasing the mesh density further produces only minor increases in peak stress.  In this case, an increase from 1134 elements per unit area to 4483 elements per unit area yields only a 1.5% increase in stress.

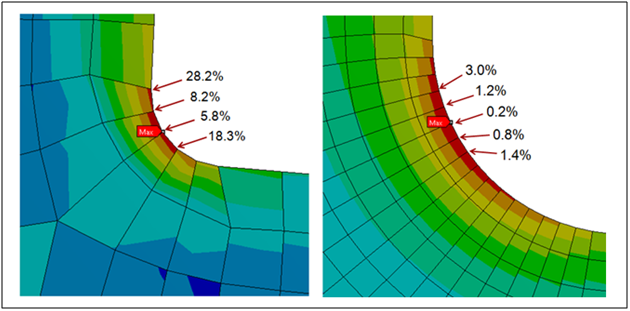
The problem with this method is that it requires multiple remeshing and re-solving operations. While this method is fine for simple models, it can be very time-consuming for complex models. However, in Ansys you can easily perform this operation automatically by using Convergence tool option.

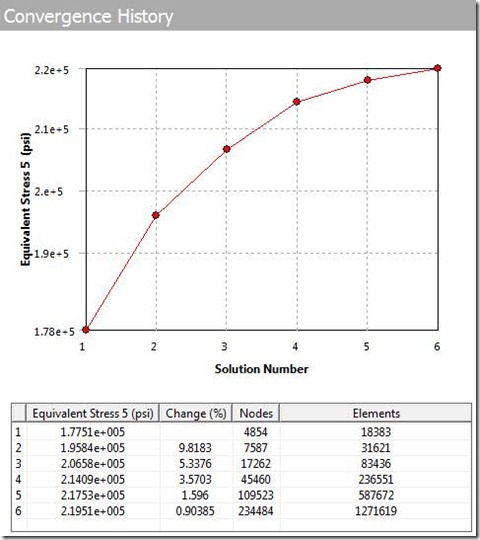
Basically, the convergence tool increases the mesh density and checks the results between each step. You can easily see how your results change depending on the element quantity.