As we engineers often start learning theories based on static problems at universities. However, once we start having a career in industry, you notice that in contrast to undergrad education we rarely used the static formulas in real life. I wouldn’t say that it is pointless to learn static problems, particularly they are the main structures of our engineering knowledge. On the other side, as Vasily Grossman said “Everything flows” or Albert Einstein, “All things in our universe are constantly in motion”, besides their philosophical meanings, we would all agree that most of the mechanical problems are dynamic and somehow they are subjected to altered forces/stress/pressure. As an academic who has been working with fatigue problems for more than 10 years, I will be talking about an in-depth understanding of fatigue. The fatigue series will be divided into 4 articles;
- The first one is Introduction to Fatigue
- we will follow with Understanding of Fatigue Life Theories
- then, Experimental Applications of Fatigue
- at last, Fatigue Fractures
History
One of the first studies in history about how metals behave under dynamic loads was completed by August Wöhler, a railway engineer, 1852-1869 and during his axle investigations interestingly he found that;
- Materials can be subjected to failure by repeating stress that is lower than static strength
- Stress amplitude is critical to determine whether the material withstands or not.
- The higher the maximum stress the system has, the lower the stress amplitudes the material can accommodate.

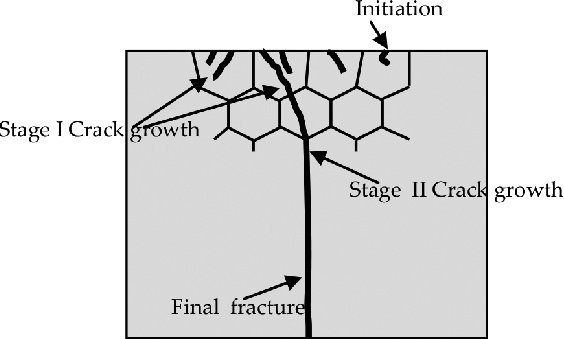
Absolutely, these findings were groundbreaking at that time and he published a number of articles and reports explaining the details of his experimental outcomes. Later on, in the 1900s, metal fatigue earned particular attention from scientists and it was explained that fatigue damage starts on the surface of the material by slip lines formed on the surface of grains. The slip lines eventually develop cracks. Once a crack reaches a considerable depth, this crack propagates across the material until the section is reduced and static failure takes place.
Wöhler was representing his results in tables, however, Spangenber, who was kind of Wöhler’s assistant, plotted the tabulated results in stress and life axis. After that moment, this method became very famous and named SN/Wöhler curves since 1936.
Fatigue Mechanism
Although a number of explanations existed about fatigue crack mechanism, in general, there is a common phenomenon, “initiation, propagation and failure”. Materials under cycling/alternating loads are subjected to stress variations (compression/tension). These variations generate microcracks that can propagate in intergranular (between the grains) or transgranular (crossing from grains) ways. By the time these micro-cracks become larger, they result in failures in the material.
Fatigue in materials due to repeated application of loads can occur in different forms; mechanical fatigue,
creep-fatigue (repeating forces in conjunction with high-temperature) and thermomechanical fatigue (the combination of temperature fluctuation and mechanical fatigue). For example, Bhopal Disaster was one of the biggest disasters in history due to thermomechanical fatigue.
In fatigue life formulations, stress level and loading conditions are often expressed with maximum stress, minimum stress, mean stress and stress amplitude. The figure below shows schematically the main parameters used in fatigue theories.
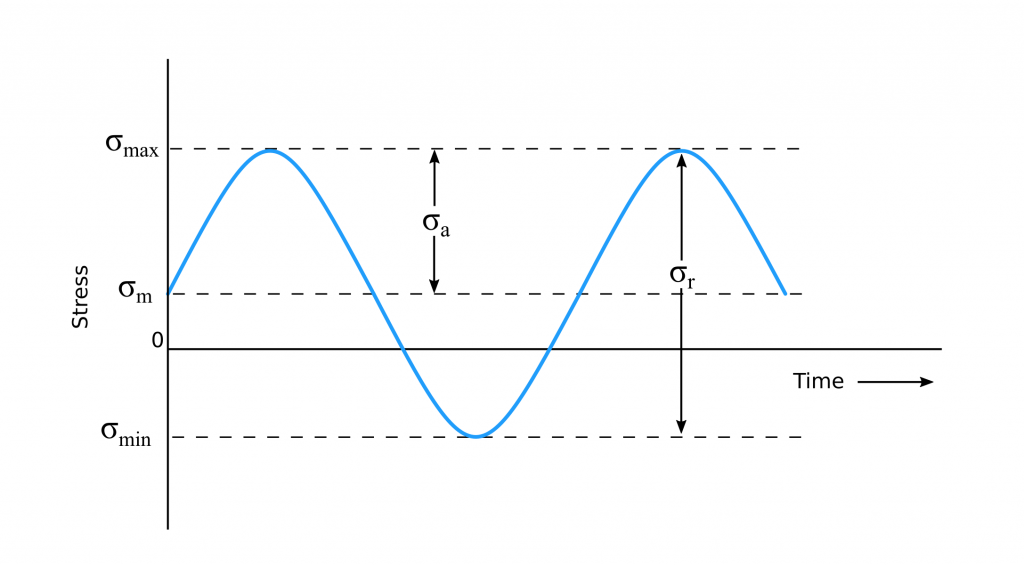
\sigma_{max}= Maximum \ stress \\
\sigma_{min}= Minimum \ stress \\
\sigma_{a}= Stress\ amplitude \\
\sigma_{r}= Stress\ range =\sigma_{max}-\sigma_{min} \\
\sigma_{m}= Mean \ stress=\frac{\sigma_{max}+\sigma_{min}}{2}
Lastly a stress ratio (R) is defined to characterize the fatigue loading condition.
R=\frac{\sigma_{min}}{\sigma_{max}}R=-1 is fully reversed loading in which the material is subjected to the same amount of compression and tension stress alternatingly. R=1 is a static loading because this means that the maximum and minimum stresses are equal. R=0 is zero-based loading where the stress range varies between zero and positive/negative values.
References
1-O. Sunar, D. Fletcher and A. Beagles, “Laboratory assessment of arc damage in railway overhead contact lines with a case study on copper-silver and low oxygen content copper,” in IEEE Transactions on Power Delivery, doi: 10.1109/TPWRD.2020.3032798.
2-Ö. Sunar and M. Çevik , “FATIGUE ANALYSIS OF SINGLE LEAF SPRINGS WITH FINITE ELEMENT METHOD”, Celal Bayar University Journal of Science, vol. 11, no. 1, pp. 1-6, Jul. 2015, doi:10.18466/cbufbe.34361
3-SUNAR, OZGUN (2021) Arc Damage Identification and Its Effects on Fatigue Life of Contact Wires in Railway Overhead Lines. PhD thesis, University of Sheffield.